



 |
 |  |  |

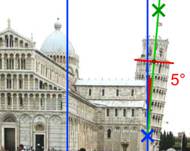
Abb. 1.1 a),b) Der schiefe Turm von Pisa
Die PISA-Studie zu Anfang dieses Jahrtausends hat gezeigt, dass etwas schief läuft mit der Mathematik in unseren Landen. Für mich kristallisieren sich aus den Analysen zwei Gründe heraus: Erstens wird in unseren Schulen der kalkülhafte Aspekt zu stark betont und eigenes Erkunden und Nachdenken zu wenig gefördert.
Zweitens lässt die Akzeptanz von Mathematik als Teil einer allgemeinen Bildung durchaus Wünsche offen, ist doch ein ungeniertes Zugeben gänzlicher Unkenntnis bei uns gesellschaftlich noch immer sanktioniert.
Dieses Buch reiht sich ein in die Bemühungen, daran etwas zu ändern.
· Neue Wege im Mathematikunterricht gehen einzelne Lehrende, Schulen oder Schulnetzwerke und Schulbuchverlage schon seit mehr als anderthalb Jahrzehnten. Langsam, ganz langsam setzt sich eine gewandelte Haltung durch. Im Bereich der Gymnasien sind Fortschritte durch die Zentralisierung des Abiturs zunächst stark behindert worden.
· Das Mathematikum in Gießen bietet Mathematik zum Anfassen. Der enorme Zulauf macht Mut und stärkt die Zuversicht, dass die Zeit für eine Wandlung der Sicht auf Mathematik reif sein könnte.
· Mathematische Kolumnen von A. Beutelspacher, E. Behrens u.a. in Zeitschriften und Zeitungen erfreuen sich großer Beliebtheit in der Leserschaft und sind z. T. inzwischen als Bücher erschienen. [Beutelspacher 1], [Behrens 1]. Überhaupt wird in meist verbaler Form dem interessierten Leser ein reichhaltiges Kaleidoskop mathematischer Anwendungen und Leckerbissen geboten.
· Das Jahr der Mathematik 2008 hat auch den Fokus auf viele sinnvolle und vielfältige Aktivitäten gerichtet.
· Einige wunderbare breit angelegte Bücher präsentieren unüberbietbar schöne Bilder aus der reichhaltigen mathematischen Welt, deren Text aber letztlich doch nur von einschlägig vorgebildeten Menschen gewürdigt werden kann. [Glaeser, Polthier] [Glaeser 1]
Genau vor diesem letzten Punkt ist dieses Buch angesiedelt. Es schließt die Lücke zwischen den darstellenden Worten mit faszinierenden Bildern einerseits und einer vertieften Darstellung für „Insider“ andererseits. Glaeser tut dies in einem großen Teil seines Geometriebuches [Glaeser 2].
Hier aber versuche ich, ein weites Spektrum der Mathematik schlaglichtartig zu beleuchten und verständlich zu machen. Dabei vertraue ich darauf, dass Sehen und Verstehen eine Einheit bilden. Die innermathematisch wichtige Formalisierung und Themen, die zu stark darin verwurzelt sind, bleiben außen vor. Die mathematischen Werkzeuge werden behutsam verwendet und befördern die Einsicht.
Dabei möchte ich herausarbeiten, inwiefern Mathematik als ein Schlüssel zur Welt, besonders unserer modernen Alltagswelt, gesehen werden kann. Unweigerlich wird dabei auch die Mathematik als kulturgeschichtliche und geistige Leistung der Menschheit erfahrbar und die ganz eigene Art der Mathematik, Probleme zu formulieren und – manchmal – zu lösen, wird deutlich.
((nachfolgender Text hier links vom Bild))
Abb. 1.2 Pythagoras im Ulmer Münster im Zusammenhang mit der Harmonielehre dargestellt.
Mit Wurzeln in hellenistischer Zeit hat Cicero in seinem Lehrplan der Humanitas gefordert, „die Seelen für die Weisheit vorzubereiten […] durch den Elementarunterricht und die freien Wissenschaften“. Augustinus, der bedeutendste Kirchenlehrer des frühen Mittelalters, hat mit Bezug auf Cicero die septem artes liberales, die sieben freien Künste vor das Fachstudium gestellt. Boëthius und Cassidorus haben sie zu Anfang des 6. Jahrhunderts in die Teile Trivium (Drei-Weg) mit Grammatik, Rhetorik und Dialektik. und Quadrivium (Vier-Weg) mit Arithmetik, Geometrie, Astronomie und Musik gegliedert. Dabei wurde die Musik im Sinne von pythagoreischer Harmonielehre gelehrt, wie Abb. 1.2 untermauert. Was gemeint ist, finden Sie in Abschnitt 6.1.4.
Für die Lehrmeister des Mittelalters gehörte Mathematik „zu den Erkenntnissen aus reiner geistiger Vernunft“. Ihre Bedeutung für die Bildung liege darin, „dass der Verstand dabei von der Materie und den unwesentlichen Eigenschaften abgezogen und im reinen schlussfolgernden Denken geübt werde“. Zitiert nach Dolch „Lehrplan des Abendlandes“ [Dolch].
In den Universitäten Europas mussten mindestens bis zum Ende des 16. Jahrhunderts sämtliche Studenten zunächst das Trivium durchlaufen. In unserem Wort trivial wirkt diese untere Stufe noch nach. Es folgte das Quadrivium mit den mathematischen Themen. Das Studium der Septem Artes schloss man mit dem Baccalaureus ab und erst dann konnte man an der medizinischen, der juristischen oder der theologischen Fakultät weiter studieren.
Eine wechselvolle Geschichte folgte, von der einfachen wöchentlichen Rechenstunde in den Gymnasien im 18. Jahrhundert bis zu der durchaus prominenten Stellung in unserer Zeit. Allerdings ging inhaltlich die Wendung zu einer stark formalen Auffassung mit ihrem Schwerpunkt in den 1970er Jahren so gründlich an den lernpsychologischen Bedingungen vorbei, dass Manfred Spitzer, Leiter des Transferzentrums für Neurowissenschaften und Lernen(ZNL) in Ulm, konstatiert, es gebe „sehr viele Menschen, die beim Anblick einer Formel in eine Art intellektueller Totenstarre verfallen“, zitiert aus einem Aufsatz zum Jahr der Mathematik in [MNU-Kolumne 2008].
Wenn die Leuphana Universität Lüneburg z. Z. als einzige Universität in Deutschland wenigstens in einem Teil des ersten Semesters ihren Studienanfängern eine allgemeine Einführung in die Wissenschaften zukommen lässt, zu der auch Mathematik für alle gehört, knüpft sie damit an eine alte Tradition an. Aus dieser Vorlesung, die ich 2007 entwickelt habe und seitdem halte, ist das vorliegende Buch entstanden. Unter www.leuphana.de/matheomnibus finden Sie die Vorlesungselemente.
Es bietet für die elf angesprochenen Themen elementare Einstiege, die Grundgedanken werden Schritt für Schritt aufgebaut. Vielfach helfen dabei Bildfolgen, die als Zugeständnis an ein Druckwerk wichtige Stationen der Gedankenführung zeigen. Sie werden aber ermuntert, auf der Website zum Buch mit interaktiven Dateien die Situationen nahtlos ineinander übergehen zu lassen und dadurch Ihr Verständnis zu vertiefen.
Abb. 1.1 b) zeigt, was gemeint ist: Nicht nur ist dort gemessen, wie schief der Turm von Pisa ist, sondern es kann im Internet an den Geraden und Punkten gezogen werden, mit eigenen digitalen Fotos kann man selbst auf Erkundungsreise gehen.
Die Adresse ist www.mathematik-sehen-und-verstehen.de .
Meist steht in den Themen ein typisches Beispiel Pate für das grundsätzliche Vorgehen. Rechnungen folgen höchstens, wenn sie kurz und elementar sind.
Mein übliches Motto „erst Verstehen, dann Rechnen“ wandle ich in diesem Buch ab in: „Besser Verstehen ohne zu rechnen als Rechnen ohne zu verstehen“.
Das Bild, das Sie nach der Beschäftigung mit einem Thema haben können, wird nicht umfassend sein, aber es soll dennoch das Richtige widerspiegeln.
Das Buch wird weder Ihnen noch Ihren Kindern – abgesehen von meinen Studierenden in „Mathematik für alle“ – in der nächsten Klausur helfen. Meine Erfahrung aber ist, dass auch der übliche mathematische Lehrstoff, wie er an Schule und Hochschule allgemein und natürlich mit rechnerischen Anteilen verlangt wird, entschieden besser bewältigt wird, wenn er mit visuell gestütztem Verstehen gepaart ist.
In kleinerer Schrift stehen Hinweise, die eher nur für Lehrende von Mathematik interessant sind.
Der große Bereich der mathematischen Knobel- und Rätselaufgaben wird überhaupt nicht angesprochen.
Aufgaben kommen nur in dem Rahmen vor, in dem sie Ihnen eine intellektuelle Freude an Ihrem eigenen Verstehen bereiten können. Lösungen sind im Anhang und auf der Website zum Buch zu finden.
Die elf Kapitel sind in unterschiedlicher Weise aufeinander bezogen.
Völlig unabhängig sind die Themen Kryptografie, Codierung, Graphentheorie und Geometrie (Kapitel 2, 3, 4, 11). Sie können einzeln gelesen werden.
Am dichtesten an schulischen Themen ist Kapitel 6: Welt der Funktionen.
Bezug darauf nehmen an wenigen Stellen die Kapitel 5 und 10, Fraktale und Stochastik.
Etwas mehr aus dem Funktionen-Kapitel 6 brauchen die Kapitel 7, 8 und 9 zur Optimierung, zu Computern in der Mathematik und zur Numerik. Sie können diese aber auch ohne Kapitel 6 mit Gewinn lesen und nur bei Bedarf nachsehen.
Das Kapitel 12 rundet ihr Bild von Mathematik, das ihnen das Buch vermitteln möchte, noch ab.
|
Abb. 1.3 |
Wie arbeitet die moderne
Kryptografie? Worauf beruht ihre Sicherheit? Was ist eine digitale
Unterschrift? Die heutige Kryptografie rechnet mit natürlichen Zahlen auf eine unübliche Weise. In dieses „modulo-Rechnen“ werden Sie mit kleinen Zahlen eingeführt, damit sich Ihnen erschließt, wie die Verschlüsselungen zustande kommen und warum Angriffe keinen Erfolg haben. |
|
Abb. 1.4 |
Was sind die Grundlagen
von Barcode und Artikelnummern? Warum knacken CDs nicht? Alte und neue Buchnummer hängen auf interessante Weise zusammen. Prüfziffern sorgen für die Sicherheit der Übermittlung. Das gilt noch mehr für den digitalen Datenfluss, den wir allenthalben in Musik, Film und Internet nutzen. Die Prinzipien sind leicht verständlich. |
|
Abb. 1.5 |
Wie kommt der Routenplaner
zum vorgeschlagenen Weg? Wie löst man logistische Probleme? Kleine Graphen sind überschaubar und an ihnen wird erklärt, wie heute mit Graphentheorie große Steuerungsprobleme gelöst werden können. Konflikt-Graphen kann man sowohl für Ampelanlagen als auch für soziologische Konstellationen einsetzen. Dieses Kapitel kann voraussetzungslos verstanden werden. |
|
Abb. 1.6 |
Was sind chaotische
Prozesse? Wie zeigt sich Mathematik in der Natur? Sie können in diesem Kapitel entweder den Blick allein auf
die Phänomene richten und über die Besonderheiten staunen, oder Sie lassen
sich auf die mathematische Sicht ein, an die Sie herangeführt werden, und
freuen sich, wie weit Sie mit dem erworbenen Wissen kommen. |
|
Abb. 1.7 |
Was sind eigentlich die
tragenden Prinzipien, mit denen es die Mathematik schafft, vielfältige
Phänomene zu modellieren? Der Funktionsbegriff ist ein universelles Werkzeug, das auch in der Schule ein großes Gewicht hat. Wenn sie diese von Bildern unterstützte Einführung verfolgen, kann sich manches in hellerem Licht zeigen. Die unübersichtlich scheinende Fülle wird gebändigt. So geht es ohne Rechnungen bis zur Ableitung und zum Integral. |
|
Abb. 1.8 |
Was sind optimale
Abmessungen und Formen? Welche wirtschaftlichen Entscheidungen versprechen
optimalen Gewinn? An einigen Beispielen wird gezeigt, wie die Mathematik bei Optimierungsproblemen hilft. Auch hier geht es nicht um Rechnung, sondern um Verstehen an geometrisch modellierten Zusammenhängen. Die Unterkapitel sind unabhängig voneinander lesbar. |
|
Abb. 1.9 |
Warum eigentlich können
Computer rechnen? Sie können ausprobieren, wie das Rechnen mit Nullen und Einsen funktioniert. Ihnen wird aber auch klar, wo die Computer ihre Grenzen haben. Die wichtigsten Software-Werkzeuge für Mathematik werden vorgestellt. |
|
Abb. 1.10 |
Wie kommt man zu Lösungen
für Probleme, die zu groß für die theoretische Bewältigung sind? Hinter vielen Anwenderprogrammen bis zu einfachen Taschenrechnern steckt Numerik, besonders wenn sie grafische Elemente haben. Einige Grundideen werden bildhaft erklärt. |
|
Abb. 1.11 |
Was sind die Grundideen
für fundierte Schlüsse in der Stochastik? Was sagt die Umfrage oder die
Messung eigentlich aus? Dieses Kapitel kann als Kompakt-Lehrbuch zur beurteilenden Statistik aufgefasst werden, in dem auch die Grundlagen aus der Wahrscheinlichkeitsrechnung sorgfältig aufgebaut werden. Damit möchte ich Ihnen eine Chance geben, unsachgemäßen Gebrauch statistischer Aussagen zu erkennnen. Stochastik gehört heute zu fast allen Ausbildungen. |
|
Abb. 1.12 |
Was ist der goldene
Schnitt? Wie prägt er sich in Architektur und Natur aus? Was haben Ellipsen
und Parabeln mit der Reflexion von Stahlung zu tun? Von Geometrie sind wir umgeben und es gibt seit Jahrtausenden Bücher darüber. Dieses Kapitel beschränkt sich auf das Verstehen des goldenen Schnittes und die Reflexion von Licht an Kurven, insbesondere Kegelschnitten. Diese verraten auch ihr Namensgeheimnis und einige gemeinsame Eigenschaften. |
|
Abb. 1.13 |
Was finden die Mathematiker
schön? Was ist Ihnen wichtig? Was ist charakteristisch für die Mathematik? Erfahren Sie von dem Wettbewerb um den schönsten mathematischen Satz. Sehen Sie zu beim wichtigsten mathematischen Handwerk, dem Beweisen. Verstehen Sie die unlösbaren Probleme der Antike und wundern Sie sich über Winkeldritteler und Kreisquadrierer. |
Als Frau in einem von Männern dominierten Gebiet gerate ich wohl nicht in den Verdacht, die Frauen unterdrücken zu wollen, wenn ich dennoch die Oberbegriffe Mathematiker, Informatiker usw. verwende. Genaueres sage ich dazu in Kapitel 12.
Wenn die Mathematiker für andere Mathematiker oder solche, die es werden wollen, Definitionen und Sätze formulieren, so verwenden sie ein ausgereiftes Fachvokabular, das letztlich eine größere Genauigkeit und den Einbezug der Grenz- und Sonderfälle erlaubt. Die kürzlich (2007) von der Deutschen Mathematiker Vereinigung DMV veröffentliche Abbrecherquote von etwa 80% in Mathematik-Studiengängen legt die Vermutung nahe, dass man lernpsychologisch nicht angemessen vorgeht. Mathematiker fürchten die Unexaktheit wie „der Teufel das Weihwasser“. Allerdings werden Studierende, die das Fach abbrechen, keine unexakten Mathematiker, sondern gar keine Mathematiker. Damit kann man dem drohenden Mathematikermangel nicht begegnen.
Wenn ich nun hier zu abstrakt, zu formal oder zu exakt formuliere, legen meine Leser vermutlich das Buch weg und mein Ziel ist nicht erreicht.
Dieses Buch ist für Menschen geschrieben, die die mathematische Komponente der Welt nicht ausblenden und einen Blick in die Mathematikwerkstatt werfen wollen. Das soll aber kein Blick in eine Zauberküche sein. Mein Anspruch ist, verständlich und dennoch mathematisch verlässlich zu reden und darzustellen.
Die Bilder locken die Gedanken, und ich wünsche Ihnen, meinen Lesern, auch eine ästhetische und intellektuelle Freude daran. Gerade dadurch, dass die Bilder beweglich gedacht sind – auf der Website zum Buch auch wirklich bewegt werden können – verlieren sie ihre Rolle als Sonderfall.
Dem dargestellten Sonderfall haftet für manche Mathematiker der Geruch der unzulässig fehlenden Allgemeinheit an und sie verwenden ausschließlich die allgemeine formale Sprache. Nun konstatiert aber W. J. T. Mitchell in seiner 2008 erschienen „Bildtheorie“ [Mitchell] für unsere Zeit die Ablösung des linguistic turn durch den pictural turn. Die Vorherrschaft der Sprache weicht der Vorherrschaft der Bilder. Es ist also wohl auch ein Zeitphänomen, dass wir uns über Bilder einem Thema besser nähern können. Die im ersten Absatz der Einleitung erwähnten Bemühungen, Aktivitäten und Bücher zeigen das auch für die Mathematik.
In besonderem Maße setzt dieses Buch Bilder über die Motivation hinaus als Denkhilfe ein. Der Leser soll sich die Mathematik im betrachteten Thema vorstellen können, was im Wortsinn vor sich hinstellen heißt.
Naturgemäß bleibt aber einiges ungesagt, genau besehen bleibt vieles ungesagt. Für die Mathematik als Ganzes ist das trivial, aber es gilt auch für die Themen, die ich Ihnen in diesem Buch zugänglich machen konnte.
Ich hoffe, aus dem
reichhaltigen Schatz der Mathematik das Richtige gewählt zu haben.
| www.mathematik-sehen-und-verstehen.de URL: https://masuv.web.leuphana.de |